帰納法・演繹法とは？考え方や活用シチュエーション例をご紹介

日常のコミュニケーションにおいて相手に自身の考えや気持ちを「伝える」ことは非常に重要になります。

しかし、「伝える」ことよりも「伝わる」ことが非常に重要になります。なぜなら、自分が伝えたことが意図しているように相手に伝わっているかはわからないからです。

相手に自分の意図した考えや気持ちが「伝わる」ために相手との「信頼関係」や「情理」が非常に大切ですが、構造的にわかりやすく伝える「論理」も同様に大切です。ここでは論理的に相手に伝える技術の一つである「帰納法」を掘り下げて述べていきたいと思います。

▼【リンクアンドモチベーションの新入社員サービス】が分かる資料はこちら​​​​​​​

帰納法とは？

■帰納法とは

帰納法は、複数の実例から共通項をまとめることによって、事実を導き出し一般化させる考え方です。統計分析にも使用される方法で、大量のデータから傾向やパターンをしっかり理解し、推論を導くことが、相手を納得させるための根拠となります。

そのため、帰納法では「蓋然性」(正しさの度合い)という概念が必要で、この蓋然性が高い推論を導き出すことができればその分論理的にも正しい可能性が高くなります。

ただ、帰納法は複数の実例、すなわち状況証拠を元に共通点を見つけ、推論を引き出す手法です。

そのため、実例や状況証拠そのものに間違いがある場合や、共通点を探し出す際や共通点から推論を導く道筋に論理の飛躍がある場合、帰納法そのものが成り立たなくなることがあります。1つでも推論に反する実例があると、推論は一気に崩壊してしまいます。

それでも帰納法が認められているのは、発信者と受信者の相互了解によってです。帰納法のロジックでは、発信者と受信者の間で納得感が醸成されていれば、別の受信者との間に納得感がなくともその発信者と受信者の間では妥当性が生まれます。

従って、帰納法は発信者と受信者が想定されることで妥当性が判断できる手法なのです。

いわゆる「経験則」に基づいた推論や「統計的手法」に基づいた結論の導出が「帰納法」の考え方を採用しています。

これは、多くの自然科学系の学問の基礎的な手法となっています。ただし、この形で得られた一般的な結論が必ずしも常に正しいとは限りません。特殊なケースが本当に全てのケースを代表しているとは限らないからです。

たとえば「1月の業績が悪い」「3月の業績が悪い」「5月の業績が悪い」という3つの事実があったとする場合、これらに共通しているのは「業績が悪い」という事実です。

つまり、共通点から導き出される結論は「上半期の業績が悪いのではないか」という一般論となります。上半期の業績が隔月ごとに悪化しているとなれば、上半期が悪化しているといわれても不思議ではありません。

ただし、ここで気を付けたいのは、他にも導き出される結論があるかもしれないということです。先ほどの結論は上半期の業績が悪いのではないかというあくまで一つの結論であって、人によっては「隔月ごとに業績が変わりやすい」といった別の結論に至ることもあるでしょう。

さらに、最も有名なケースとして挙げられるものが「カラス（烏）は全身が黒い」というものがあります。

確かに我々が日常で眼にするカラスは全て全身が黒いです。従って、殆どの人がこれは正しいと思っています。

ところが、世の中には「白黒2色」や「暗褐色に白斑」のカラスもいて、必ずしも全身が真っ黒のものだけではありません。

ただし、これは「カラス」というものの定義がどのようになってのかにもよると言えるかもしれません。動物分類学的には真っ黒ではないカラスもカラスなのかもしれないが、殆どの人にとって、真っ黒なものだけが（我々が通常認識している）カラスだと思っているため、何ら問題はないとの考え方もできるのかもしれません。

いずれにしても、「帰納法」は常にこうした要素を内在していることを認識しておく必要があります。

帰納法を用いるときに事象を整理する代表的なフレームワーク

問題の原因を特定するには、まずは起きている事象を整理する必要があります。

そのときに役に立つフレームワークが「分類」「ラベリング」「構造化」の3つです。

「分類」ではまずどのような目的で分類するのかを明確にし、似たもの同士をグルーピングしながら軸を設定します。

「ラベリング」では分類したグループごとに特徴を表すネーミングを行うことで、複雑性を縮減します。

「構造化」では分類の第一水準の分岐点を決め、さらに第二水準以降の要素を分類していくことで、関係性を分かりやすくします。

「分類」と「ラベリング」は以下の順番で同時に行っていくことが効果的です。

　　①分類の目的を明確にする（目的の明確化）
　　②似たもの同士をグルーピングしながら軸を設定する（分類の軸選定）
　　③分類後はグループごとに特徴を表すネーミングを行う（ラベリング）
　　④各グループごとに「抜け・漏れ」がないか検証する（網羅性の検証）

この手順で「分類」と「ラベリング」を行った後に、以下の手順で「構造化」していきます。

　　①目的に照らして分類の第一水準の分岐点を決める（第一水準の決定）
　　②第二水準以降の要素を更に分類していく（下位水準の分類）
　　③各要素間の水準を更に揃える（全体構成）

構造化は全体像を把握することに役立つため、コミュニケーションの際もとても重要なフレームワークです。

整理された情報をもとに、原因の特定を行うフレームワーク

起きている事象の整理ができたら、次は整理された情報を元に、問題の原因を特定します。

その際に有効なフレームワークは「切り分け」と「ビリヤード思考」です。

「切り分け」では以下手順で原因の特定を行います。

　　①何の原因究明を行うのかを明確にする（原因究明対象の明確化）
　　②問題の事実情報を整理する（事実情報の収集）
　　③IS／IS NOTによる切り分け
　　④「IS」の特性や変化情報を整理する （ISの特性や変化考察）
　　⑤推定原因を複数想定する（推定原因の列挙）
　　⑥推定原因を検証し、絞込みを行う（原因の特定）

まず、何の問題の原因を究明するのかを明らかにします。そして、その問題に対する情報から、うまくいっているものはあるのか？それと状況を比較すると問題の発生している箇所はどうか？を「3W1E」に基づき「IS／IS NOT」に切り分けます。

この手順で、問題発生部分と非発生部分の境を特定することができます。その結果から推定原因を複数想定し絞込みを行います。

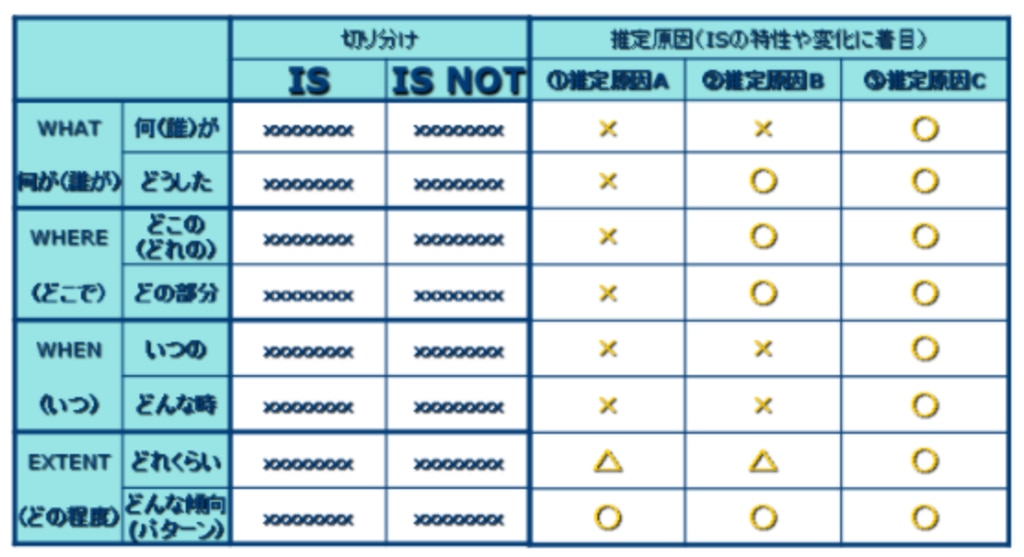
「ビリヤード思考」では、「切り分け」で見えてきた原因を元に、要素間のつながりや相互影響関係を考え、最も全体にインパクトを与える関係性を特定します。 手順としては以下です。

　　①何の対策を考えるのか、何の問題解決をするのかを明確にする（思考目的の明確化）
　　②目的達成に影響する事象を諸要素に分ける（要素分解）
　　③分解した要素間の関係性（影響関係）を考える（要素間関係の分析）
　　④最も全体にインパクト（影響）与える関係性を特定する（キーファクターの特定）

解決策を洗い出すフレームワーク

問題の原因を特定できれば、次は解決策を洗い出すことが必要です。その際に有効なのが「マトリクス」というフレームワークです。複数の項目を掛け合わせることで、可能性を創出したり、縮減させます。

全ての組み合わせパターンを見ていくことで新たな解決案を見出したり、逆に組み合わせる意味のないものを排除して必要なものだけに絞り込むことができます。

方法としては、以下手順で行っていきます。

　　①どの組み合わせ（マトリクス）を考えるのか、目的を明確にする（目的の明確化）
　　②「縦軸」「横軸」を設定する（組み合わせ軸の設定）
　　③各々のマス目（組み合わせ）パターンの中身を検討する（組み合わせパターンの網羅）
　　④「新しいパターンの検討」或いは「想定パターンの絞込み」を行う（可能性の創出・可能性の縮減）

まず、洗い出したい目的を明確にし、今まで分類やラベリングなどのフレームワークで整理してきた情報を元に、適した縦軸と横軸を設定します。

その上で各々のマス目（組み合わせ）パターンの中身を検討し、「新しいパターンの解決策の検討」或いは「必要のないパターンの排除」を行います。

制約条件を踏まえて最も有効な解決策を絞り込むフレームワーク

実行するためには洗い出した解決策の選択肢から、最も有効な解決策を絞り込む必要があります。その際に効果を発揮するフレームワークが「選択基準」です。

実際の手順は以下です。

　　①何のための選択を行うのかを明確にする（目的の明確化）
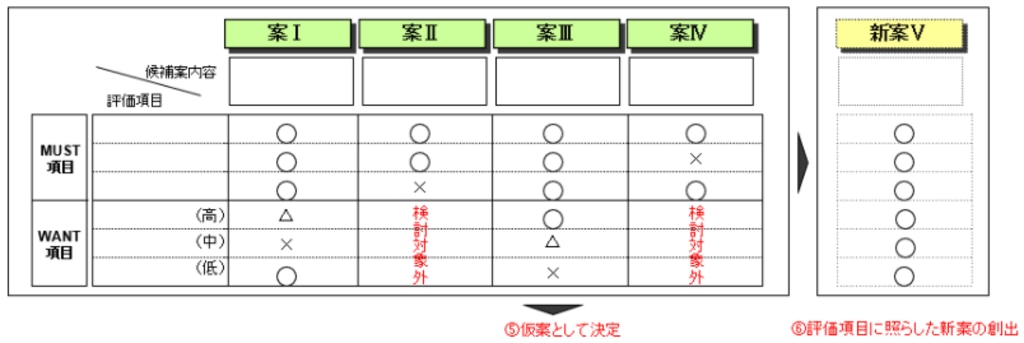
　　②仮の候補案（選択案）を列挙する（候補案の列挙）
　　③候補案を評価する「評価項目」を列挙する（評価項目の列挙）
　　④評価項目の優先順位付けを行う（MUST／WANTの設定）
　　⑤評価項目に照らして合わせて候補案の絞込みを行う（候補案の決定）
　　⑥評価項目に照らして合わせて新代替案を創り出す（新案の企画）

まずは目的を明確化し、マトリクスによって選択された解決策、その候補案を評価する「評価項目」をリストアップします。

この評価項目には目的が達成された時の具体的な姿や達成基準を数値化した指標や、期限、投入できる金額、使用できる人員などの制約項目を入れます。

評価項目がリストアップできたら、項目の中で優先順位を決めます。目的の達成のために絶対にはずせない項目(MUST項目)、可能ならば充たしたい項目(WANT項目)がどれなのか決め、そのなかでも重要度(高、中、低など）の分類を行うことで解決策を絞り込みやすくなります。

解決策の中で最も条件に当てはまるものを仮案として選び、それを元に最終的な解決策を決定します。

帰納法と演繹法の違い

■演繹法とは

帰納法に対して、演繹（えんえき）法という思考法が引き合いに出されることがありますが、演繹法は帰納法とは結論の導き出し方が異なります。

しかしどちらの思考法も結論を導き出すという点では活用できるので、帰納法、演繹法ともに扱えることが好ましいです。両方を使い分けることによって、効率良く結論が導き出せます。 

では、演繹法という思考法について説明していきます。演繹法の特徴はルールや法則に基づく物事から結論を導き出すということです。

帰納法は複数の事実や事例から一般論となり得る結論を導き出しますが、演繹法は一般論に基づく物事に当てはめて結論を導き出すという違いがあります。

たとえば演繹法の場合、「野菜はビタミンを含む」という一般論に対して、「ニンジンは野菜である」という物事を当てはめた結果、「ニンジンにはビタミンを含む」という結論になります。

対する帰納法の場合、「ニンジンにはビタミンがある」という事実や事例に対して「ニンジンは野菜」という共通点を導き出した結果、「野菜はビタミンを含む」という結論（一般論）となります。

このように演繹法と帰納法は結論の導き出し方が逆になっているので、うまく使い分けることができれば、より正確な結論を導き出すことができます。

こうした「帰納法」に対応する手法が「演繹法」と言われているものです。これは、「一般的な原理等から、特殊な結論を導き出す手法」である。その代表的な手法として「三段論法」が挙げられます。即ち、

　　大前提：ＡはＢである。
　　小前提：ＢはＣである。
　　結論　：従って、ＡはＣである。

という論法です。この手法は幅広く世の中一般で使用されています。

この「演繹法」については、前提となっている一般的な原理が正しければ、結論も常に正しいことになります。

数学における証明においては、一般的に「演繹法」が使用されています。

そうした中にあって、「数学的帰納法」については、限られた自然数の例から、次々と命題の正しさが証明されていき、一般的な結論を導き出していることから、それがいかにも「帰納的」に見えるということで「帰納法」という名称が付されています。

以前に「数学記号の由来」シリーズの研究員の眼の中で、例えば「∞（無限大）」の記号を導入したとして紹介したジョン・ウォリス（John Wallis）が初めてこの手法に「induction」の名称を使用したとされています。

ところが、「数学的帰納法」によって証明される結論は、その手法の使用に過ちがなければ常に正しいことになるし、その証明方法はまさに「演繹的」であるとの言い方ができるので、実は「演繹法」の一種ではないかとも言われています。

ところで、「数学的帰納法」を最初に使用したのは、17世紀の著名なフランスの数学者ブレーズ・パスカル（Blaise Pascal）で、彼が1654年に発表した「三角形に関する論文（Traite du Triangle Arithmetique）」においてであるとされてます。

数学の世界におけるもう一つの有名な証明法である「背理法」（帰謬法）については、紀元前300年頃に活躍したユークリッド（Euclid）が「素数が無数にある」ことの証明で使用しています。この「背理法」と比較すると「数学的帰納法」は相当に新しい手法であることがわかります。

以上ここまで、「帰納法」と「演繹法」について述べてきました。数学の世界の証明は、ある意味で全て「演繹的」であるといえるが、その証明すべき命題や仮説を導き出す際には経験則等に基づいた「帰納的」な考え方が採用されています。

「演繹法」で使用されている原理等も、今は自明な命題や前提として認識されているかもしれませんが、帰納的に導かれてきたものであるともいえます。

その意味で、２つの手法は相互に関連しあって、ともに重要な位置付けを有するものとなっています。

ただし、前提として選定した一般論や普遍的事実に偏った主観が混じってしまうと、論理が破たんするため注意が必要です。

逆をいえば、前提の選定さえ間違えなければ、そのプロセスの特性上、非常に強い説得力をもつ推論方法であるともいえます。

帰納法があくまでも統計的結果を指し示すに過ぎないのに対し、演繹法の結論はより真実に近いものと考えられるのです。

ただし、この2つは優劣のあるものではありません。論理的推論が必要となる状況や説得する相手の傾向によって使い分けることが望ましいでしょう。

■帰納法の考え方

では、帰納法と演繹法それぞれの特徴を理解したところで、実際にビジネスシーンでの利用を想定してみましょう。一般的に帰納法は調査による統計などを使用する場合に適しており、演繹法はアイディアが正しいことを証明するときに効果的といえます。

例えば、帰納法は

• 「男女数百人に結婚に対するアンケートをとった結果、約7割の人が結婚をすることに肯定的だった」
• 「結婚したい人は毎年少しずつ増加している」
• 「別のアンケートでは婚活サービスを利用した結婚が3年連続過去最高」

という3つのデータがある場合、これらを前提として「結婚市場は今後も拡大し続ける」という推論を導き出すことができるでしょう。

このようにマーケティングやアンケートの結果を重視し、論理展開を行うのが帰納法です。前提に普遍的事実があるかないかよりも、観察した結果から導き出される納得感を重視するため、一定以上のサンプルや事例の量があれば帰納法は効果的といえるでしょう。

これに対して演繹法は、前提となる原理原則に関する正確な知識が必要です。そのため、新商品やサービスの開発時に効果的といえるかもしれません。

新しい商品やサービスを開発するためには、その素となる知識や技術が必要で、いくら商品やサービスが画期的であっても、知識や技術を当てはめることができなければ商品として成立しえないでしょう。

また、物事を戦略的に考えたり、組織構成を立案したりといった場合にも演繹法が適していると考えられます。

つまり、それまでの実績をもとに次の戦略を決定し、利益（結論）につなげるという流れです。失敗が許されない責任重大な立場におかれるほど、演繹法を使うシーンが増えてくるでしょう。

営業やマーケティングなど数多くのサンプルから傾向を導き出すときは帰納法を、事業方針や戦略立案など過去の実績の上に次の展開を積み重ねるときは演繹法を使うなど、状況に合わせて使い分けていきましょう。

▼【リンクアンドモチベーションの新入社員サービス】が分かる資料はこちら

帰納法を活用するシチュエーション例

帰納法を活用する場合、さまざまな事実や事例から見つかる共通点を突き止め、そこから根拠となる部分を導き出して一般論となる結論にたどり着くのが目的です。

帰納法を用いた実例は多くあるので、コツが分かればうまく活用することができるでしょう。

それでは、帰納法の実例をご紹介しましょう。

■例1｜売り上げを伸ばしているチェーン店

• 「競合小売りチェーン店Aは組織開発に力を入れたことで、売り上げを伸ばしている」
• 「競合小売りチェーン店Bは組織開発に力を入れたことで、売り上げを伸ばしている」
• 「競合小売りチェーン店Cは組織開発に力を入れたことでで、売り上げを伸ばしている」

という3つの実例がありました。

3つの実例に共通していることは、「全ての競合小売りチェーン店で組織開発に力を入れた」ことです。つまり、一般論となる結論は、「自社も組織開発に力を入れる」というものになります。

ただし、単純に考えればこの結論で良いと思うかもしれませんが、あくまで一つの結論でしかなく例外があることを忘れてはいけません。

一つの結論を導き出したうえで、「例外があるとするなら、何があるのか？」ということを考えることで、さらに売り上げを伸ばすチャンスがあるかもしれません。

■例2｜リンクアンドモチベーションの考え方

• 「リンクアンドモチベーションにはモチベーションエンジニアリングを用いるモチベーションエンジニアがいます」
• 「リンクアンドモチベーションのワークはモチベーションエンジニアリングを用いています」
• 「リンクアンドモチベーションモチベーションエンジニアリングによって組織と個人に変革の機会を提供し、意味のあふれる社会を実現します」

という3つの実例がありました。

3つの実例に共通していることは、「リンクアンドモチベーションモチベーションエンジニアリングによって組織と個人に変革の機会を提供し、意味のあふれる社会を実現します」ということです。

つまり、一般論となる結論は、「モチベーションエンジニアリングによって組織と個人に変革の機会を提供できる技術」というものになります。

■例3｜プロジェクト

• 「ミーティングで共有しようとしている資料はプロジェクト全体に影響を与える重要な内容が含まれている」
• 「ミーティングで共有しようとしている資料は見ただけでは伝わりにくいニュアンスが含まれている」
• 「新しくプロジェクトに参加したメンバーとの目的や意識の統一を図る必要性がある」

という3つの実例がありました。

3つの実例に共通していることは、「メールで共有するよりも顔を合わせたミーティングの方が今後のプロジェクトの進行がスムーズになる」ことです。

つまり、一般論となる結論は、「ミーティングをセッティングする」というものになります。

演繹法を活用するシチュエーション

■例1｜因果関係に当てはめる

演繹法は因果関係によって結論が導き出されることがあります。 広告費用と売り上げの関係に注目した例をみてみましょう。

まず、過去のデータから広告を30％増やすことによって売り上げが35％上がるという因果関係が導き出されたとしましょう。

この場合、当てはめる因果関係は「広告を30％増やすことによって売り上げが35％上がる」ことになり、その因果関係に当てはめて考える事柄が「今回のプロモーションの売り上げ目標は+35％」ということになります。

したがって、導き出される結論は「今回のプロモーションで広告を30％増やす」ことになるでしょう。このように因果関係から演繹法を使うことで、提案の根拠や結果の予測によって結論がスムーズに導き出されます。

■例2｜ルールに当てはめる

次はルールによる演繹法の思考です。もしも自社の投資の意思決定に対して、「リターンが120％以上見込めるのであれば投資するが、それ以下なら投資しない」というルールがあったとします。

しかし、投資をしても「リターンが90％しか見込めない」ということが分かったとします。

そこから導き出される結論は、「今回の投資は見送る」です。

このように判断と意思決定によって演繹法に活用できます。

記事まとめ

帰納法と演繹法による思考法は、結論の求め方は異なりますが、さまざまな場面で役に立つ方法です。

演繹法はルールや法則に基づく物事に当てはめて結果を導き出すものですが、帰納法は複数の事実や事例から共通点を導き出し、一般論となる結論にたどり着くための方法です。

この2つの思考法を状況に応じて使い分けることで、より正確な結論を導き出すことができるでしょう。

ただ、記事の初めにもお伝えした通り、相手に伝える上では信頼関係や感情も非常に大切です。その点を理解した上でこれらの方法を用いて相手にわかりやすく伝える工夫をしましょう。

▼【リンクアンドモチベーションの新入社員サービス】が分かる資料はこちら